Gait change in tongue movement
[ad_1]
Declaration
The University of Canterbury’s Human Ethics Committee (HEC) approved ethics for this study (HEC 2012/19). All experiments were performed in accordance with the relevant named guidelines, regulations, and agreed-upon procedures listed in the HEC 2012/19 document. Each participant provided informed consent before participating in the experiments. Participants were compensated with $40 New Zealand Dollars worth of local Westfield mall vouchers.
Participants
We recorded 11 participants (9 female and 2 male). (Note: Because articulometry experiments are long and demanding, worldwide median participant counts are small (5 as of 202044). All but one of the participants were native monolingual North American English (NAE) speakers, and the other was a native bilingual NAE and French speaker. Participants reported normal hearing following the Nobel45 paradigm, where participants are asked about any difficulty hearing, any difficulty following television programs at a socially acceptable volume, and their ability to converse in large groups or noisy environments.
Materials
Setup included an NDI Wave EMA machine with 100 Hz temporal resolution and 16 five degrees-of-freedom (5D) sensor ports. Setup also included a General Electric Logiq E 2012 ultrasound machine with a 8C-RS wide-band micro-convex array 12 (times) 22 mm, 4–10 megahertz imaging frequency transducer. Audio was collected using a USB Pre 2 pre-amplifier connected to a Sennheiser MKH-416 short shotgun microphone mounted to a Manfrotto “magic arm†for directional control. Ultrasound data were captured using an Epiphan VGA2USB Pro frame grabber connected to a MacBook pro (late-2013) with a solid-state drive. The USB-Pre 2 audio output and NDI wave machine were connected to a Windows 7 desktop computer with the NDI Wavefront control and capture software installed. This setup allows simultaneous ultrasound, EMA, and audio recording of participants. In this study, the ultrasound measurements were used for visual confirmation of tongue movements only.
Stimuli
We selected eight one- or two-word utterances, or token types, with double-flap sequences (e.g. ‘auditor’), and embedded them in carrier phrases that have no adjacent tongue motion-generating consonants (e.g. ‘We have auditor books’). The stimuli are all listed in Table 1. Stimuli were chosen to allow for a variety of surrounding vowel contexts, while simultaneously keeping the experiment short enough to allow the equipment to work effectively.
The phrase structures we used were designed to ensure that speakers would place primary stress on the syllable before the first flap, a context in which speakers are most likely to produce flap sequences46. We introduced different speech rates by having participants hear reiterant speech (e.g. ‘ma ma ma ma ma ma’) produced at one of five different speech rates (3–7 syllables per second). In our experiment, we had participants listen to this reiterent speech, and then read one of the eight phrases displayed on a computer screen at that reiterent speech rate to the best of their ability. Each example was randomly presented as 40 phrases per block, with 10 blocks in total, such that the entire task took 45 min to complete.
Setup and procedure
After completing initial screening, each participant was seated in a comfortable chair and heard a detailed description of the experimental procedure. An ultrasound transducer was held in place beneath the chin using a soft, non-metallic stabilizer47, allowing participants’ tongue movements to be recorded using ultrasound. The ultrasound measurements were used for visual confirmation of tongue movements, but were otherwise not included in the analysis. Five-dimensional (5D) electromagnetic articulometry (EMA) sensors were taped to the skin over the mastoid processes behind the ears and the nasion. Sensors were then taped and glued midsagitally to the upper and lower lips on the skin next to the vermillion border using Epiglu. One sensor was then glued to the lower incisor, and three to the tongue: One approximately 1 cm away from the tongue tip, one at the back or tongue dorsum, just avoiding the gag reflex, and one in between the two or tongue body. Tongue sensors were then coated in Ketac, a two-part epoxy cement normally used in dental implants. Both the Epiglu and Ketac are slowly broken down by saliva, allowing about 1 h of experiment time.
Once sensors were connected, the MKH-416 short shotgun microphone attached to a Manfrotto magic arm was placed on the opposite side of the head from the NDI wave electric field generator. The microphone was far enough away to avoid electro-magnetic interference with the NDI sensors, but close enough to reduce the acoustic interference from the many machine fans used to cool equipment during the recordings. The NDI wave recordings were captured at 100 cycles per second (Hz), and the audio recordings were synchronously captured at 22,050 Hz using 16 bit pulse-code-modulation (a standard .wav file format).
Once the setup was complete, participants read 10 blocks each containing the 8 sentences in Table 1, at 5 different speech rates, presented on a computer using Psychopy248. We induced different speech rates by having participants hear reiterant speech (e.g. ‘ma ma ma ma ma ma’) produced at one of five different speech rates (3, 4, 5, 6, or 7 syllables per second) before being asked to read the relevant phrase at the preceding reiterant speech rate. Within each block, sentences and speech rates were randomly presented. Participants read sentences at the reiterant speech rate as instructed and to the best of their ability. In the event of sensor detachment, the area around the sensor was quickly dried with a paper towel, and the sensor was reattached with Epiglu only, within 1 mm of the original attachment point. No sensor was reattached a second time.
Once the experiment was complete, the participant was asked to hold a protractor between their teeth with the flat end against the corners of the mouth, and three (3) 10-s recordings of the occlusal (bite) plane were recorded. Setup took between 30 and 45 min; recording took about 45 min; recording of the occlusal plane, palate, and head rotation took no more than 10 min; and removal of sensors took 5 min. The entire process was typically completed within 2 h.
Data processing
EMA data were loaded from NDI-wave data files, and smoothed with a discrete cosign transform technique that effectively low-pass-filters the data and restores missing samples using an all-in-one process49,50. This process was implemented through MVIEW51. Data were then rotated to an idealized flat (transverse cut) occlusal plane with the tongue tip facing forward. This was accomplished using the recorded occlusal plane and the recorded planar triangle between the nasion and two mastoid processes, allowing all of the participants’ data to be rotated and translated to a common analysis space. Tongue palate traces were generated using the highest tongue sensor positions along the midsagittal plane, correcting for extreme outliers.
Acoustic recordings were transcribed, isolating the phrases in one transcription tier, the vowel-flap-vowel-flap-vowel sequences under analysis in a second tier, and the two flap contacts in a third tier. Flap contacts were identified by the acoustic amplitude dip46, or by ear if the flap was approximated enough to not have an amplitude dip (such approximants were rare, accounting for less than 10% of the data).
In order to compare different speech rates, the acoustic and vocal tract movement information was subdivided into 31 time slices: Eleven (11) from the onset of the first vowel to the point of lowest acoustic intensity of the first flap, 10 more from that point to the point of the lowest acoustic intensity of the second flap, and from there, 10 more to the end of the following vowel. The entire time span constitutes the duration of each token type. These Procrustean fits allowed comparison of tongue motion and acoustic information at the same relative timing regardless of speech rate, and an example is illustrated in Fig. 1.
Procrustean fit time slices for ‘editor’, as spoken by participant 3, block 10, at 3 syllables/s.
Acoustic cues were chosen because our previous research showed that flaps in English can be categorized in at least four patterns. Two of them, alveolar-taps and post-alveolar taps, involve tongue tip and blade motion towards the teeth or hard palate, making light contact, and moving away again. Two others, up-flaps and down-flaps, involve the tongue making tangential contact with the teeth or hard palate31. These subphonemic difference mean that it is impossible to identify flap contact through articulatory gesture identification tools such as FindGest51. However, there is almost always a direct and simultaneous relationship between the point of lowest amplitude in the acoustic signal and the timing of tongue to palate/teeth contact during flap production46. This makes acoustic cues the most suitable method of isolating the underlying articulatory motion patterns for this dataset.
Visualization
Movement data from these Procrustean fits were visualized on millimetre-grid graphs. The graphs show the palate and position traces of the tongue tip, tongue body, tongue dorsum, lower incisor, upper lip, and lower lip throughout token production for each reiterant speech rate from 3 to 7 syllables/s. These graphs were produced for each participant and token type, with movement traces averaged over all the blocks. Versions of this graph tracing each block separately were used to identify cases where EMA sensors became unglued from the participants’ tongues, or sensor wires had tiny breakages. These tokens were excluded from analysis. Lastly, visual comparison of the different speech-rate traces revealed a wide variety of tongue motion pattern differences between participants, token types, and speech rates.
Analysis: displacement range and speech-rate range
In order to test the prediction that speakers can shift tongue motion patterns in flap sequences to gain access to wider speech-rate ranges, we needed to compare duration to tongue motion patterns. Duration was measured from the start of the first vowel to the end of the third vowel—the span shown in Figure 1. However, there were so many different tongue motion pattern differences between participants, token types, speech rates, and recording blocks that we needed two equations to linearize this complexity of motion. These equations convert all of the above complexity into a cumulative measure of tongue motion displacement that accounts for both the sum of distance of motion and the sum of angular displacement.
Equation (1) captures the sum of the linear distance of motion along the course of any given vocal tract sensor’s motion through the Procrustean fit.
$$begin{aligned} D = sum _{i=1}^{30} d _{vec {(i,i+1)}}. end{aligned}$$
(1)
Each vector is calculated from the linear displacement, in a Euclidean plane, of a vocal tract sensor between adjacent Procrustean time slices. The value D captures the sum of the 30 displacements d in each vector in order from (d_{vec {(1,2)}}) through to (d_{vec {(30,31)}}), where the subscript numbers represent the relevant position of the sensor at that Procrustean time slices.
Equation (2) captures the sum of the angular displacement along the course of any given vocal tract sensor’s motion through the Procrustean time slices.
$$begin{aligned} Theta = sum _{i=1}^{29} |theta _{vec {(i,i+1)},vec {(i+1,i+2)}}|. end{aligned}$$
(2)
Each vector is the same as for Eq. (1). The value (Theta) captures the sum of the 29 angles ((theta)) between each vector in order, from (|theta _{vec {(1,2)},vec {(2,3)}}|) through to (|theta _{vec {(29,30)},vec {(30,31)}}|), where the subscript numbers represent the relevant position of the sensor at that Procrustean time slice. The (theta) is always the smallest of the absolute value of two possibilities, and so is never more than (pi) radians.
The process of computing each of these formulas is visualized in Fig. 2.
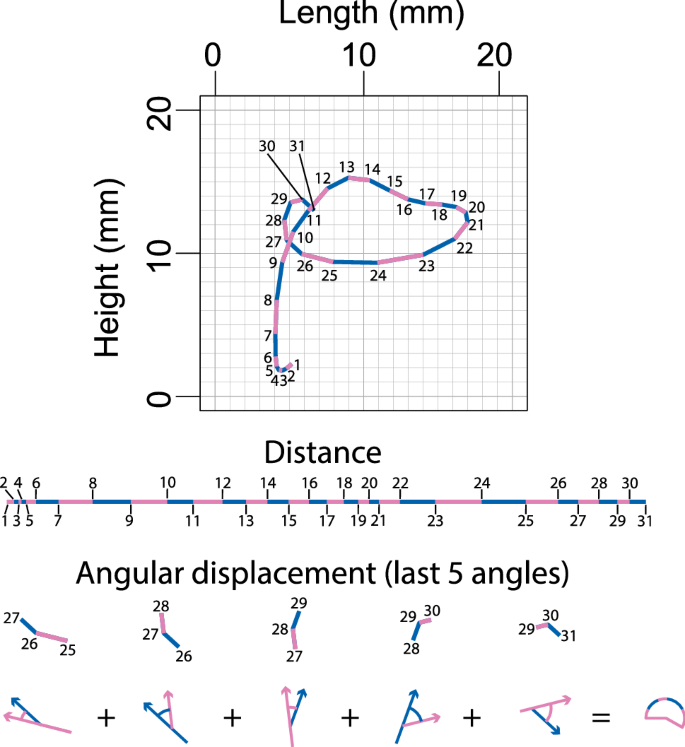
Illustration of the calculation process Eqs. (1) and (2). The top graph shows tongue tip motion for the average (mean) position of each instance of tongue-tip motion (facing right) for participant 9, token type ‘we have auditor books’, and reiterant speech at 3 syllables/s. The middle section shows a lining up of the path shown, giving the sum distance (for all values of i = 1–30 in Eq. 2). The bottom of the figure shows the visual process for calculating angular displacement for part of the tongue motion (showing only values of i = 25–29 in Eq. 1).
Because the measures for angular displacement (Eq. 2) are in radians, and distance (Eq. 1) are in millimetres, their scales are unrelated to each other. To resolve this issue, we applied z-scores to each, as seen in Eq. (3).
$$begin{aligned} z = (x – mu ) / sigma , end{aligned}$$
(3)
where (x) is the result from the relevant equation (Eq. 1 or 2), using the mean ((mu)) divided by the standard deviation ((sigma)). All z-scores were computed across the entire dataset (all token instances and all participants). This allows the results of both equations to be added together in a way that weights distance and angular displacement equally, giving us a measure of total displacement.
Displacement range
We then computed displacement range by comparing mean displacements for each participant (11 participants) and token type (8 types) produced at 3 syllables/s, and subtracting the mean displacements produced at 7 syllables/s. This provided us with displacement range data to compare to the average (mean) of the duration, grouped by participant (11 participants), token type (8 types), and reiterant speech rate (5 rates). We ran generalized linear mixed-effects models (GLMMs) as seen in Eq. (4).
$$begin{aligned} Duration&sim Displacement~Range~times ~Reiterant~Speech~Rate~ nonumber &quad +(1~+~Displacement~Range~|~Participant) end{aligned}$$
(4)
In this equation, written in R code52, Duration is equal to token utterance time, Displacement Range is the displacement range described above, Reiterant Speech Rate is one of 3–7 syllables/second, and Participant is the unique identifier for each research participant.
We ran this model for four measures of displacement range: (1) tongue tip only, (2) tongue tip and body (tongue front), (3) the whole tongue, and (4) the whole vocal tract. These four options were made as the tongue tip visually showed the most differences in displacement, followed by the tongue body, the tongue dorsum, and the lips/jaw which moved the least.
We then made ANOVA comparisons of the GLMMs ran with our four displacement ranges, and the tongue-front displacement range produced was the best fit. The model’s r2 was 0.816 for the fixed effects (r2m), and 0.892 when the random effect of participant variability was included (r2c). This comparison process allowed us to exclude sensors that did not add any statistically significant information to our analysis. Nevertheless, it must be recognized that the tongue tip and tongue body sensors naturally incorporate some jaw motion data as the tongue rides on the jaw.
Tongue-front displacement range
In more detail, the equation for tongue tip and body (tongue-front) displacement is seen in Eq. (5).
$$begin{aligned} T = z((z(Theta TT) + z(D TT) + z(Theta TB) + z(D TB)). end{aligned}$$
(5)
This equation shows z-scored tongue front [tongue tip (TT) and tongue body (TB)] distance (d) and angular displacements ((theta)) summed together and then z-scored again so that the resulting sum displayed standard deviations in our graphs. We named this equation (Eq. 5) tongue-front displacement, and the displacement range—comparing mean displacements for each participant (11 participants) and token type (8 types) produced at 3 syllables/s, and subtracting the mean displacements produced at 7 syllables/s—is the tongue-front displacement range. This tongue-front displacement range, when graphed along with duration, allowed us to graph the relationship between tongue-front displacement range and speech-rate, revealing speech-rate range. This graph not only revealed speech-rate range, but allowed us to identify the shortest and longest displacement ranges and show the actual tongue motion patterns for both groups in a different figure.
Analysis: critical fluctuations
But in order to demonstrate that tongue-front displacement range is also associated with an increased likelihood of a speaker having two stable gaits instead of just one, we needed to compare critical fluctuations through the time-course of token production with tongue-front displacement range.
This equation for calculating critical fluctuation needed to work with a short-term time series—our 31 Procrustean time slices. One such equation is the fluctuation equation (F) from Schiepek and Strunk’s real-time monitoring of human change processes39. The fluctuation equation identifies positions of critical instability that indicate upcoming potential phase change by incorporating components of the 1st through 3rd derivative of the short-term time series. Differences in the patterns of phase change at different speech rates indicate that the changes in displacement also correspond to gait-change. This equation can work with as few as 7 data points. The fluctuation equation (Eq. 6) is as follows:
$$begin{aligned} F = dfrac{sum nolimits _{i=1}^{l} dfrac{|x_{n_{k+1}}-x_{n_{k}}|}{(n_{k+1}-n_{k})}}{s(m-1)}. end{aligned}$$
(6)
Unlike the formula in Schiepek et al.39, n is transformed by its relative position in time, as shown in the waveform in Fig. 1, such that the sum of the n values remains equal to m, but the ratio reflects the information required for maximum accuracy of the fluctuation calculation. The value (x_{n}) is the nth number value in the time series. The value k indicates then number of points of return, that is, the number of times the time series values change direction. The value i represents the periods between points of return. The value l is the total number of periods within the window. The value m is the number of measurement points within a moving window, in our case 7. The value (m-1) is the number of intervals between the measurement points, in our case 6. The value s = (x_{max} – x_{min}); (x_{min}) is the smallest value of the scale, in our case (-pi), and (x_{max}) is the largest value of the scale, in our case (pi). This guarantees that the range for F is always a value between 0 and 1 (even with the n transformation above).
Higher F-values indicate greater critical fluctuation, which itself corresponds to more production effort as compared to lower F-values. Lastly, F-values were calculated over two sets of data: (1) Tongue tip and (2) Tongue body ({theta _{vec {1}}, ldots , theta _{vec {30}}}), tracking through time slices of 7 vectors from ({1, ldots ,7}) through to ({23, ldots ,30}) such that these vector sets supply x in Eq. (6). The (theta) values were used because with a maximum range of (2pi) they meet the requirement for Eq. (6). Tongue tip and tongue body were used because they were the measurement sensors that carried the significant information for tongue-front displacement. These values were summed, and then divided by 2 to represent the tongue-front displacement fluctuations with a theoretical range of (0 leqslant F leqslant 1). The algorithm is shown visually in Fig. 3, along with example paths and the fluctuation (F) value for each of them.
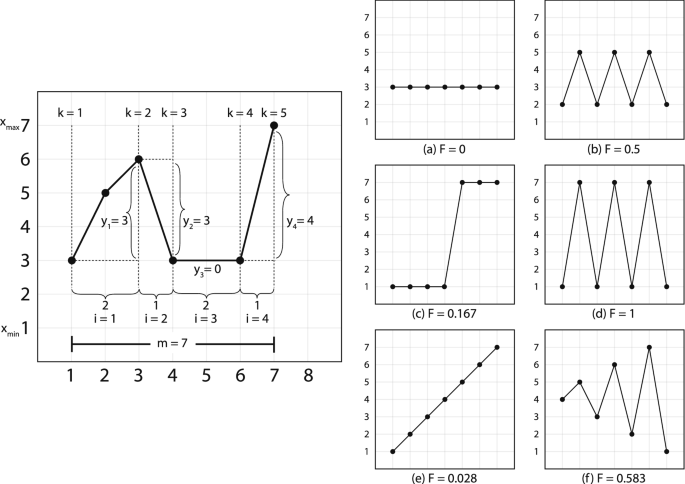
Calculation of F (Eq. 6). Left hand side shows a visualization of how to implement the algorithm. Right hand side shows six examples of the output of the algorithm. Note that the algorithm produces higher numbers from a combination of rate and amplitude of each change in direction. Image modified from Figs. 2 and 3 in Schiepek and Strunk39, used by permission following STM permissions guidelines.
Next, and in order to make sense of this highly non-linear data, we ran a generalized additive mixed-effects model (GAMM) on the data shown in Eq. (7)53,54. GAMMs are extremely effective for the analysis of non-linear data, and are therefore highly suitable for the analysis of the critical fluctuations captured in Eq. (6).
$$begin{aligned} gam(Fluctuation&sim te(FTS,~TFd)~nonumber &quad + s(FTS,~TFd,~Participant,~bs =“fs”, m = 1)nonumber &quad + s(SPS,~Participant,~bs =“re”)~nonumber &quad + s(Token type,~Participant,~bs =“re”). end{aligned}$$
(7)
Equation (7), written in R-code52, describes a generalized additive mixed-effects model, comparing Fluctuation based on tongue-front displacement (TFd) and the fluctuation time slice position (FTS), forming a 3-dimensional tensor (te) field [te(FTS, TFd)]. The random effects factor out participant variability in a 3-dimensional tensor field [s(FTS, TFd, Participant, bs = “fsâ€, m = 1)], as well as random-effect smooths for syllables per second [s(SPS, Participant, bs = “reâ€)], and token type [s(Token type, Participant, bs = “reâ€)]. In order to correct for autocorrelation effects, we ran the GAMM, calculated an estimate for a start value (rho) from that first run, and provided that (rho) to a second run of the GAMM model, along with an indicator identifying the first position of our time slices. This removes most of the autocorrelation, maximizing the accuracy of the resulting statistical model output.
Equation (7) produces an output that shows the relationship between critical fluctuation, token position, and tongue-front displacement range, highlighting regions of significant difference. And with these methods, we were able to identify whether tongue-front displacement range affected speech-rate range, and whether tongue-front displacement range had any influence on the timing slice positions of critical fluctuations.
[ad_2]

